#
Hashrate Ratio
The hashrate ratio is the quotient a of Sha256t hashrate \mathfrak{h}_Y and Verushash v2.2 \mathfrak{h}_X:
a = \frac{\mathfrak{h}_Y}{\mathfrak{h}_X}
#
Hashrate Ratio Boost
The Janusscore satisfies
S(\mathfrak{h}_X,\mathfrak{h}_Y)=\gamma(a)S(\mathfrak{h}_X,\mathfrak{h}_X)with
\gamma(a) :=
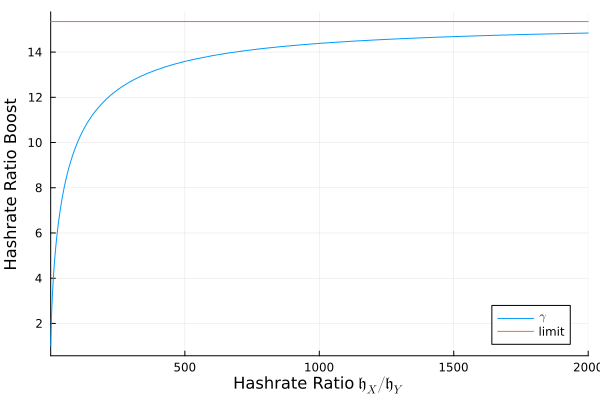
\frac{ a\big((c+1/a)^{0.3}-c^{0.3}\big)}{(c+1)^{0.3}-c^{0.3}}for a\ge 1 (again mind the small range [1,(1-c)^{-1}] where the reasoning is not correct). We therefore call \gamma(a) the hashrate ratio boost for hashrate ratio a. It is a multiplicative factor applied to a hypothetical reference Janusscore S(\mathfrak{h}_X,\mathfrak{h}_X) to express S(\mathfrak{h}_X,\mathfrak{h}_Y). The function \gamma looks like this:
c = 0.005
beta = 0.7
f(a) = a*((c+1/a)^(1-beta)-c^(1-beta))
g(x)=f(x)/f(1)
using Plots
p = plot(g, xlim=[1,2000], label = "\$\\gamma\$", ylabel = "Hashrate Ratio Boost", xlabel = "Hashrate Ratio \$\\mathfrak{h}_X/\\mathfrak{h}_Y\$")
hline!([15.35], label="limit")There is a limit on the hashrate ratio boost:
\begin{align*}
\lim_{a\to\infty} \gamma(a) &= \lim_{a\to\infty}a\big((c+1/a)^{0.3}-c^{0.3}\big)/((c+1)^{0.3}-c^{0.3})\\
&=\lim_{a\searrow 0}\frac{((c+a)^{0.3}-c^{0.3}\big)}{a}/((c+1)^{0.3}-c^{0.3})\\
&=\lim_{a\searrow 0}0.3(c+a)^{-0.7}/((c+1)^{0.3}-c^{0.3})\\
&=0.3c^{-0.7}/((c+1)^{0.3}-c^{0.3})\\
&\approx 15.35,
\end{align*}where we used L'Hôpital's rule in the third step and finally plugged in the constant c = 0.005. This means that hashrate ratio boost cannot go above \approx 15.35 no matter how much Sha256t hashrate is thrown into the game. The higher the hashrate ratio of GPU/CPU hashrates, the more CPU, i.e. Verushash v2.2 hashrate becomes the bottleneck.
This is intended and protects Warthog against ASICs applied to Sha256t. Such mining behavior will suffer heavily from being bottlenecked by CPU hashrate.
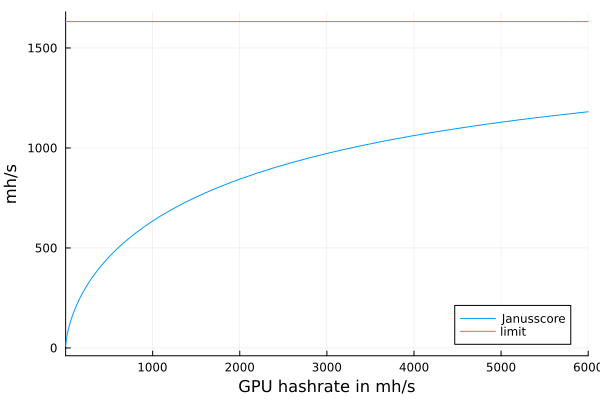
For example in the setting where the CPU hashrate is 40mh/s we have the following Janusscore curve and no ASIC on SHA256t can increase it above the limit of \approx 1632.15 mh/s.
c = 0.005
hx = 40
S(hx, hy) = hy * 10 * ((c + hx/hy)^0.3 - c^0.3)/3
p = plot(hy->S(hx,hy), xlim=[1,6000], label = "Janusscore", ylabel = "mh/s", xlabel = "GPU hashrate in mh/s")
hline!([15.35*S(hx,hx)], label="limit")
#
Estimating Hashrate Ratio from mined blocks
The conditional density p_{Y,a} of Y given (X,Y)\in A_{\tau} and Y\in [c,c+\tfrac{1}{a}] is proportional to
\begin{align*}
p_{Y,a}(y)&= \frac{e^{-y}\int_{-\log(\tau)-0.7y}^{\infty}e^{-x}\textnormal{d}x}{\int_{-\log(c+\frac{1}{a})}^{-\log(c)}\int_{-\log(\tau)-0.7y}^{\infty}e^{-x}\textnormal{d}x\textnormal{d}y}\\
&= \frac{\tau e^{-0.3y}}{\int_{-\log(c+\frac{1}{a})}^{-\log(c)}\tau e^{-0.3y}\textnormal{d}y}\\
&= \frac{e^{-0.3y}}{\int_{-\log(c+\frac{1}{a})}^{-\log(c)}e^{-0.3y}\textnormal{d}y}\\
&= 0.3\frac{e^{-0.3y}}{(c+\frac{1}{a})^{0.3}-c^{0.3}}\\
\end{align*}for y\in[c, c+\frac{1}{a}]. Note that again this does not depend on the target \tau. The conditional expectation is
\begin{align*}
\mathbb{E}\big[Y| (X,Y)\in A_{\tau} \land Y\in [c, c+\tfrac{1}{a}]\big]
&= \frac{\int_{-\log(c+\frac{1}{a})}^{-\log(c)}0.3e^{-y}e^{-0.3y}\textnormal{d}y}{(c+\frac{1}{a})^{0.3}-c^{0.3}}\\
&= \tfrac{0.3}{1.3}\frac{(c+\frac{1}{a})^{1.3}-c^{1.3}}{(c+\frac{1}{a})^{0.3}-c^{0.3}}\\
\end{align*}If we have N blocks mined from a specific address we can consider their Sha256t hashes y_1,\ldots,y_N to compute the empirical expectation (mean) \bar{y}=N^{-1}\sum\limits_{i=1}^{N} y_i.
The method of moments can be used to get an estimate \hat a of the hashrate ratio a from observed Sha256t average \bar{y}. To do this we must find a such that the empirical expectation observed from the blocks and the conditional expectation match:
\begin{align*}
\text{Find $a\in[1,\infty]$ such that}&\quad\bar{y} = \tfrac{0.3}{1.3}\frac{(c+\frac{1}{a})^{1.3}-c^{1.3}}{(c+\frac{1}{a})^{0.3}-c^{0.3}}\\
\end{align*}Unfortunately this can only be solved numerically, we cannot express the solution analytically. Since the hashrate ratio a is in the range [1,\infty], the maximal conditional expectation is attained for a=1, if we observe an empirical mean \bar y larger than this number
\tfrac{0.3}{1.3}\frac{(c+\frac{1}{1})^{1.3}-c^{1.3}}{(c+\frac{1}{1})^{0.3}-c^{0.3}}\approx 0.269we just estimate \hat a=1, otherwise we solve the above equation numerically. In the following code we cap estimation at factor 100000:
from math import exp
from scipy.optimize import fsolve
# example usage
def get_miningratio(sha256t_list):
"""Function to determine the hashrate ratio
from a list of observed sha256t values
:sha256t_list: list of numbers in [0,1] corresponding to sha256t hashes
:returns: estimate of hashrate ratio
"""
y_avg=sum(sha256t_list)/len(sha256t_list)
c = 0.005
p = lambda a: 0.3/1.3*((c+a)**1.3-c**1.3)/((c+a)**0.3-c**0.3)
threshold = p(1/100000)
if y_avg<threshold:
return 100000
elif y_avg >p(1):
return 1
f = lambda a: p(a)-y_avg
return 1/fsolve(f, [threshold, 1])[0]
# example usage
sha256t_list=[0.025,0.014,0.032]
get_miningratio(sha256t_list)